Patch

Patch is introduced Walmsley et al.[1]. In this implementation, it defines fiber stress \(\sigma_f\) as function of natural fiber strain \(\varepsilon_f\). The Patch is used in a Wall object which uses the one-fiber model to relate fiber stress to tension.

Module summary

Tags: Patch

The Patch describes the relationship between \({\sigma}_f = {\varepsilon}_f\).

Parameters

Am_ref [\(m^2\)]: float

Reference wall area at \(l_{s} = l_{s,ref}\).

V_wall [\(m^3\)]: float

Wall volume

v_max [\(\mu m/s\)]: float

Maximum shortening velocity

l_se0 [\(\mu m\)]: float

lgth of the series elastic element, i.e. \(l_{s} -l_{si}\) for which stress is zero.

l_s0 [\(\mu m\)]: float

Reference sarcomere lgth for which at \(A_m (l_{s,ref}) = A_{m,ref}\).

dl_s_pas [\(\mu m\)]: float

Nonlinear exponent of Titin stress

Sf_pas [Pa]: float

Linear ECM stress coefficient

fac_Sf_tit [-]: float

Contribution factor of titen stress multiplied with Sf_act

k1 [-]: float

Nonlinear exponent ECM stress component

tr [s]: float

Contraction time constant

td [s]: float

Relaxation time constant

time_act [-]: float

Relative contraction duration

Sf_act [Pa]: float

Linear active stress component

dt [s]: float

Activation delay relative to intrinsic activation

C_rest [-]: float

Rest contractility

l_si0 [\(\mu m\)]: float

Reference lgth for zero-active-stress

LDAD [s]: float

strain dependend activation duration

ADO [s]: float

activation duration offset

LDCC [-]: float

stretch dependend contractility coefficient

Sf_pasMaxT: float

Maximum ecm stress (adaptation sens variable)

Sf_pasActT: float

Active weighted passive stress (adaptation sens variable)

FacSf_actT: float

Active stress (adaptation sens variable)

LsPasActT: float

Weighted sarcomere lgth average (adaptation sens variable)

adapt_gamma: bool

Adaptation constant

Signals

Signals are arrays. Each point in the array represents a point in time with step-size controlled by the solver.

l_s [\(\mu m\)]: array

Sarcomere lgth

l_si [\(\mu m\)]: array

State variable: Intrinsic sarcomere lgth

LsiDot [\(\mu m/s\)]: array

State variable: Intrinsic sarcomere lgth time-derivative

C [-]: array

State variable: contraction curve

C_dot [1/s]: array

State variable: contraction time-derivative

Am [m:sup:2]: array

Patch mid-wall area

Am0 [m:sup:2]: array

Patch mid-wall zero-stress area

Ef [-]: array

Natural strain

dA_dT [m / N]: array

Area-tension derivative

Sf [Pa]: array

Total fibre stress at mid-wall

Sf_pasT [Pa]: array

Total passive stress at mid-wall

SfEcm [Pa]: array

Total ECM stress at mid-wall

dSf_dEf [Pa]: array

Total stiffness coefficient

dSf_pas_dEf [Pa]: array

Total passive stiffness coefficient

SfEcmMax: array

Adaptation: Maximum ECM stress

Sf_actMax: array

Adaptation: maximum active stress

Sf_pasAct: array

Adaptation: active-weighted passive stress

LsPasAct: array

Adaptation: active-weigthed sarcomere lgth

Physiological Background

The Patch module

The Patch module is a phenomenological model of the sarcomere. A sarcomere is modelled as a three-element Hill contraction model (Fung[2]), in which the elastic element (with length \(l_{se}\)) and contractile element (with length \(l_{si}\)) in series are in parallel with an elastic element (\(l_s=l_{se}+l_{si}\)), which is calculated as

(1)\[l_s = l_{s,ref} e^{\varepsilon_f}\]

in which \(l_{s,ref}=2\) is the reference length of the sarcomere at reference wall area \(A_{m,ref}\). Fiber strain is derived from mid-wall area \(A_m\), wall curvature \(C_m\), and wall volume \(V_{wall}\) (Lumens et al.[3]). In the Patch module, the fiber strain \(\varepsilon_{\text{f}}\) is the input and is calculated by the Wall module.

(2)\[\varepsilon_{\text{f}} = {\frac{1}{2}}\ln \left( {{\frac{{A_{\text{m}} }}{{A_{\text{m,ref}} }}}} \right)\]

The intrinsic sarcomere length is a delayed image of the sarcomere length and is given by the following differential equation

(3)\[ \frac{dl_{si}}{dt} = v_{max} \cdot (\frac{l_s-l_{si}}{l_{se,iso}} -1 )\]

in which \(v_{max}\) is the unloaded sarcomere shortening rate and \(l_{se,iso}\) the length of series elastic element. The total sarcomere length will decrease at a rate proportional to the length of the series elastic element when the cell is unloaded [deTOMBE]. Total fibre stress is the sum of two stress components, an active stress generated by sarcomere contraction, and a passive stress arising from structures such as the ECM and titin. Both passive and active stress depend upon the length of the sarcomere.

(4)\[ \begin{align}\begin{aligned}\sigma_f = \sigma_{pas} + \sigma_{act}\\\frac{d\sigma_f}{d\varepsilon_f} = \frac{d\sigma_{pas}}{d\varepsilon_f} + \frac{d\sigma_{act}}{d\varepsilon_f}\end{aligned}\end{align} \]

Active material behavior

The active stress depends also on time through a contractility parameter \(C\). Contractility is a phenomenological quantity representing the density of cross-bridges formed in the sarcomere. There is a resting value of contractility, which may be non-zero. This can represent residual cross-bridge formation during diastole. Contractility increases when the tissue is activated. Activation is smooth and has a rise and decay phase with different time constants. The rate of change of contractility increases with sarcomere length (Kentish et al.[4]). Active stress increases with contractility, contractile element length and series elastic element length. Based on these assumptions, the contractility curve \(C\) is implemented as a state-variable and given by

(5)\[ \frac{dC}{dt} = \frac{1}{\tau_{rise}} C_L(l_{si}) \cdot f_{rise}(t) - \frac{1}{\tau_{decay}} C \cdot f_{decay}(X)\]

with

(6)\[ \begin{align}\begin{aligned} \tau_{rise}=0.55 \cdot T_r \cdot t_{duration}\\ \tau_{decay}=0.33 \cdot T_d \cdot t_{duration}\end{aligned}\end{align} \]

This function uses the function \(f_{rise}\) to modulate the rise of the contractility and \(f_{decay}\) to modulate the decay of contractility.

The first is given by:

(7)\[ f_{rise}(x_{rise}(t))=0.02x_{rise}^3 \cdot (8-x_{rise})^2 \cdot e^{-x_{rise}}\]

(8)\[ x_{rise}(t)=\min(8,\max(0,\frac{t-t_{act}}{\tau_{rise}}))\]

Crossbridge formation function \(C_L (l_{si})\)

(9)\[ C_L (l_{si} )=\tanh\left(LDCC \cdot (l_{si}-l_{si,0})^2 \right)\]

Decay function \(g(X)\)

(10)\[ f_{decay}(x_{decay}(t))=0.5+0.5 \cdot \sin\left(\text{sign}(x_{decay}) \min(\pi/2,\left|x_{decay}\right|) \right)\]

(11)\[ x_{decay}(t)=(t-t_{act}-t_{duration})/\tau_{decay}\]

From the contractility curve, the total active stress is calculated using

(12)\[ \sigma_{act}=S_{f,act} \cdot C \cdot 1.51 (\frac{l_{si}}{l_{si,0}} - 1)\cdot l_{se}/l_{se,iso}\]

(Source code, png, hires.png, pdf)

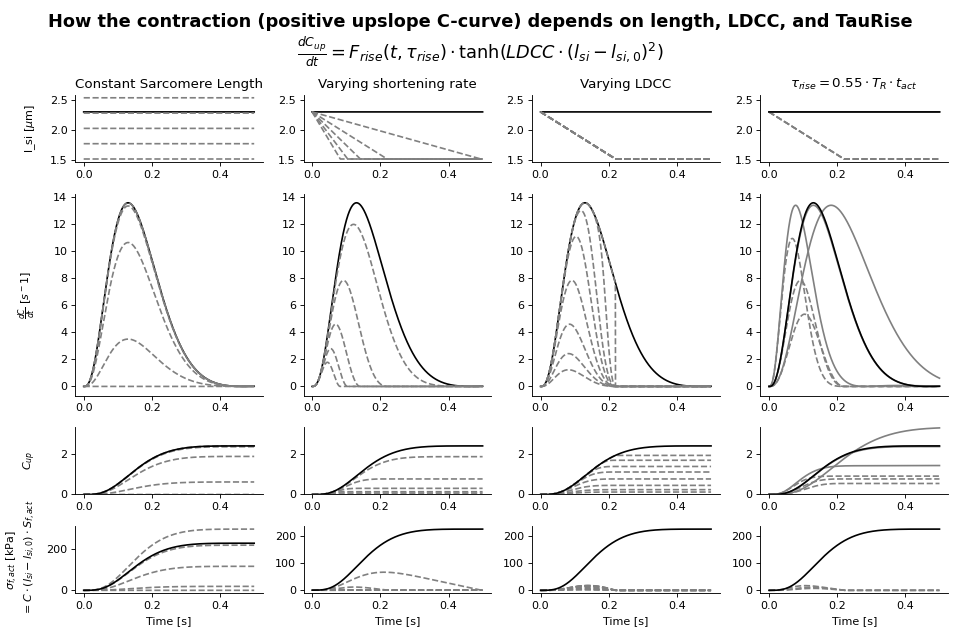
Fig. 12 Sensitivity analysis of the upslope of the C-curve. The black line represents a reference curve at \(l_s=2.25 {\mu}m\).

Passive material behavior

The passive stress \(\sigma_{pas}\) in this model is given by two separate components describing the stress of the extracellular matrix, \(\sigma_{ecm}\), and the stress of titin, \(\sigma_{tit}\).

(13)\[ \sigma_{pas} = \sigma_{ecm} + \sigma_{tit}\]

These passive stress-strain equations are given by

(14)\[ \sigma_{ecm} = S_{f,pas} \cdot ((\frac{l_s}{l_{s,0pas}})^{k_1} - 1)\]

(15)\[ \sigma_{tit} = 0.01 \cdot S_{f,act} \cdot ((\frac{l_s}{l_{s,0pas}})^{2 \cdot l_{s,ref} / d l_{s,pas}} - 1)\]

(Source code, png, hires.png, pdf)

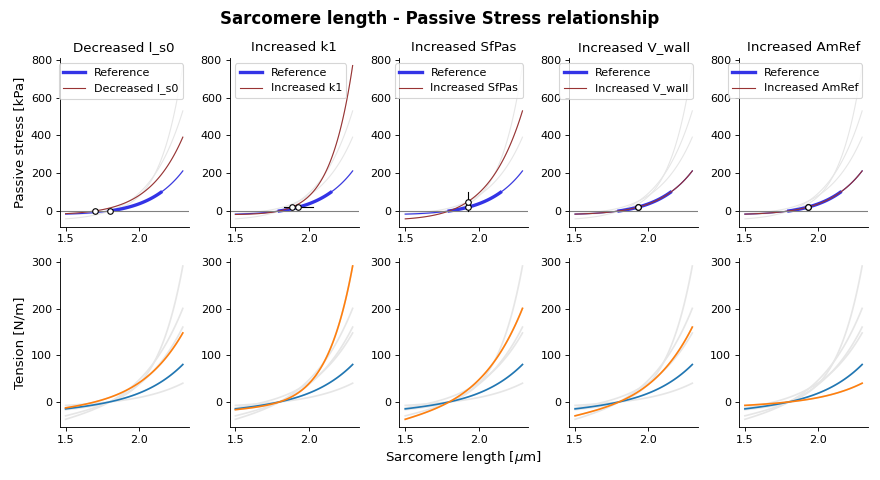
Fig. 14 Passive stress-strain relation as function of sarcomere length

(Source code, png, hires.png, pdf)

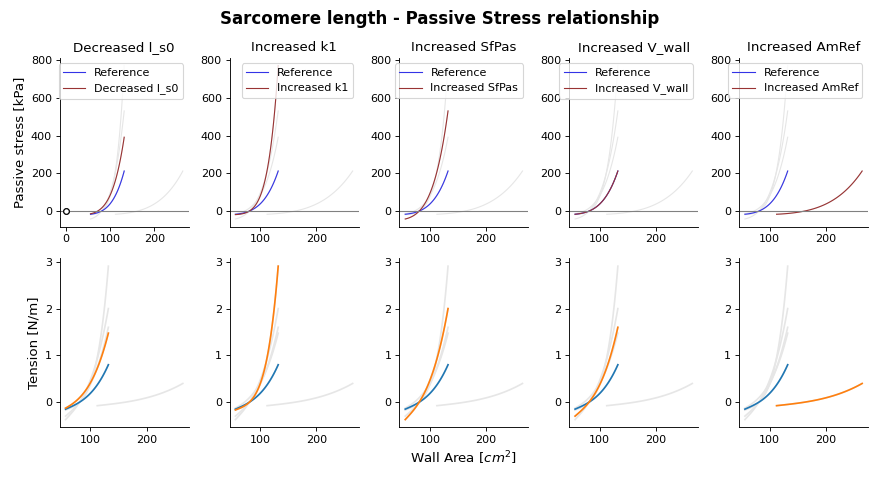
Fig. 16 Passive stress-strain relation as function of wall area

Assumptions

Not Included in this Version of the Model:

• Force-frequency relationship (force of contraction increases with heart rate).

• Electrophysiology model, only imposed activation times.

• Biophysics / energetics of calcium transient, cross-bridge formation, etc - currently, this is modelled phenomenologically and availability of ATP is assumed to be infinite.

• Sympathetic / para-sympathetic stimulation of cardiomyocytes.

References

[1]

John Walmsley, Theo Arts, Nicolas Derval, Pierre Bordachar, Hubert Cochet, Sylvain Ploux, Frits W. Prinzen, Tammo Delhaas, and Joost Lumens. Fast simulation of mechanical heterogeneity in the electrically asynchronous heart using the multipatch module. PLOS Computational Biology, 11(7):1–23, 07 2015. URL: https://doi.org/10.1371/journal.pcbi.1004284, doi:10.1371/journal.pcbi.1004284.

[2]

Yuan-Cheng Fung. Mathematical representation of the mechanical properties of the heart muscle. Journal of biomechanics, 3(4):381–404, 1970.

[3]

Joost Lumens, Tammo Delhaas, Borut Kirn, and Theo Arts. Three-wall segment (triseg) model describing mechanics and hemodynamics of ventricular interaction. Annals of biomedical engineering, 37:2234–2255, 2009.

[4]

Jonathan C Kentish, HE Ter Keurs, Lucio Ricciardi, JJ Bucx, and MI Noble. Comparison between the sarcomere length-force relations of intact and skinned trabeculae from rat right ventricle. influence of calcium concentrations on these relations. Circulation research, 58(6):755–768, 1986.

circadapt.components.patch.Patch(model[, ...])

The Patch describes the relationship between \({\sigma}_f = {\varepsilon}_f\).