Patch2022

circadapt.components.patch.Patch2022(model)

Patch2022 is based on Patch in Walmsley 2015.

List of relevant tutorials

Patch is introduced [Walmsley2015]

Documentation

Patch2022 is based on Patch in Walmsley 2015.

Parameters

Am_ref: float

Reference wall area at \(l_{s} = l_{s,ref}\).

V_wall: float

Wall volume

v_max: float

Maximum shortening velocity

l_se: float

lgth of the series elastic element, i.e. \(l_{s} -l_{si}\) for which stress is zero.

l_s0: float

Reference sarcomere lgth for which at \(A_m (l_{s,ref}) = A_{m,ref}\).

l_s0: float

Zero passive stress lgth

dl_s_pas: float

Sf_pas: float

Linear ECM stress coefficient

k1: float

Nonlinear exponent ECM stress component

tr: float

Contraction time constant

td: float

Relaxation time constant

time_act: float

Relative contraction duration

Sf_act: float

Linear active stress component

dt: float

Activation delay relative to intrinsic activation

C_rest: float

Rest contractility

l_si0: float

Reference lgth for zero-active-stress

LDAD: float

lgth dependend activation duration

ADO: float

activation duration offset

LDCC: float

lgth dependend contractility coefficient

Sf_pasMaxT: float

Maximum ecm stress (adaptation sens variable)

Sf_pasActT: float

Active weighted passive stress (adaptation sens variable)

FacSf_actT: float

Active stress (adaptation sens variable)

LsPasActT: float

Weighted sarcomere lgth average (adaptation sens variable)

adapt_gamma: bool

Adaptation constant

Signals

Signals are arrays. Each point in the array represents a point in time with step-size controlled by the solver.

l_s: array

Sarcomere lgth

l_si: array

State variable: Intrinsic sarcomere lgth

LsiDot: array

State variable: Intrinsic sarcomere lgth time-derivative

C: array

State variable: contraction curve

C_dot: array

State variable: contraction time-derivative

Am: array

Patch mid-wall area

Am0: array

Patch mid-wall zero-stress area

Ef: array

Natural strain

T: array

Mid-wall tension

dA_dT: array

Area-tension derivative

Sf: array

Total fibre stress at mid-wall

Sf_pasT: array

Total passive stress at mid-wall

SfEcm: array

Total ECM stress at mid-wall

dSf_dEf: array

Total stiffness coefficient

dSf_pas_dEf: array

Total passive stiffness coefficient

SfEcmMax: array

Adaptation: Maximum ECM stress

Sf_actMax: array

Adaptation: maximum active stress

Sf_pasAct: array

Adaptation: active-weighted passive stress

LsPasAct: array

Adaptation: active-weigthed sarcomere lgth

The myocardial tissue module Patch takes as its inputs mid-wall segment area A_m and time t, and outputs fibre stiffness (dA_m)/dt and zero-tension reference area A_m0. Each initialized module object consists of two state variables, namely the contractile element length l_si and the contractility curve C. Myocardial tissue is deformable (soft) and incompressible. Sarcomere mechanics are assumed homogeneous in a single segment, meaning one single sarcomere represents the entire segment. A sarcomere is modelled as a three-element Hill contraction model [FUNG ], in which the elastic element (with length l_se) and contractile element (with length l_si) in series are in parallel with an elastic element (l_s=l_se+l_si), which is calculated as

(1)\[l_s = l_{s,ref} \sqrt{A_m/A_{m,ref}}\]

in which \(l_{s,ref}=2\) is the reference length of the sarcomere at reference wall area A_(m,ref). The intrinsic sarcomere length is a delayed image of the sarcomere length and is given by the following differential equation

Active behavior

(2)\[ \frac{dl_{si}}{dt} = v_{max} \cdot (\frac{l_s-l_{si}}{l_{se,iso}} -1 )\]

in which v_max is the unloaded sarcomere shortening rate and l_(se,iso) the length of series elastic element. The total sarcomere length will decrease at a rate proportional to the length of the series elastic element when the cell is unloaded [deTOMBE]. Total fibre stress is the sum of two stress components, an active stress generated by sarcomere contraction, and a passive stress arising from structures such as the ECM and titin. Both passive and active stress depend upon the length of the sarcomere.

(3)\[\sigma_{tot}=\sigma_{act}+\sigma_{pas}\]

Active stress generation The active stress depends also on time through a ‘contractility’ parameter. Contractility is a phenomenological quantity representing the density of cross-bridges formed in the sarcomere. There is a resting value of contractility, which may be non-zero. This can represent residual cross-bridge formation during diastole. Contractility increases when the tissue is activated. Activation is smooth and has a rise and decay phase with different time constants. The rate of change of contractility increases with sarcomere length [KENTISH]. Active stress increases with contractility, contractile element length and series elastic element length. Based on these assumptions, the contractility curve C is implemented as a state-variable and given by

(4)\[ \frac{dC}{dt} = \frac{1}{\tau_{rise}} C_L(l_{si}) \cdot F_{rise}(t) - \frac{1}{\tau_{decay}} C \cdot g(X)\]

with

(5)\[ \tau_{rise}=0.55 \cdot T_r \cdot t_{duration} \tau_{decay}=0.33 \cdot T_d \cdot t_{duration}\]

activation function F_rise (t)

(6)\[ F_{rise}(t)=0.02x^3 \cdot (8-x)^2 \cdot e^(-x)\]

(7)\[ x(t)=min(8,max(0,\frac{t-t_{act}}{\tau_{rise}}))\]

Crossbridge formation function C_L (l_{si} )

(8)\[ C_L (l_si )=tanh(4(l_si-l_(si,0) )^2 )\]

Decay function g(X)

(9)\[ g(X)=0.5+0.5 \cdot sin(sign(X) min(\pi/2,abs(X)) )\]

(10)\[ X(t)=(t-t_{act}-t_{duration})/\tau_{decay}\]

From the contractility curve, the total active stress is calculated using

(11)\[ \sigma_{act}=S_{f,act} \cdot C \cdot 1.51 \frac{l_{si}}{l_{si,0}} - 1)\cdot l_{se}/l_{se,iso}\]

(Source code, png, hires.png, pdf)

Passive behavior

(12)\[ \sigma_{ecm} = S_{f,pas} \cdot ((\frac{l_s}{l_{s,0pas}})^{k_1} - 1)\]

(13)\[ \sigma_{tit} = 0.01 \cdot S_{f,act} \cdot ((\frac{l_s}{l_{s,0pas}})^{2 \cdot l_{s,ref} / d l_{s,pas}} - 1)\]

(14)\[ \sigma_{pas} = \sigma_{ecm} + \sigma_{tit}\]

(Source code, png, hires.png, pdf)

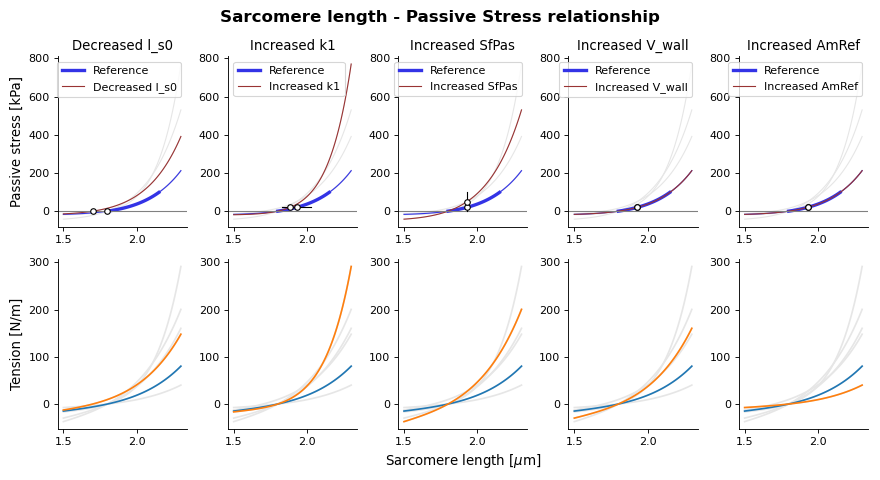
Passive stress-strain relation as function of sarcomere length

(Source code, png, hires.png, pdf)

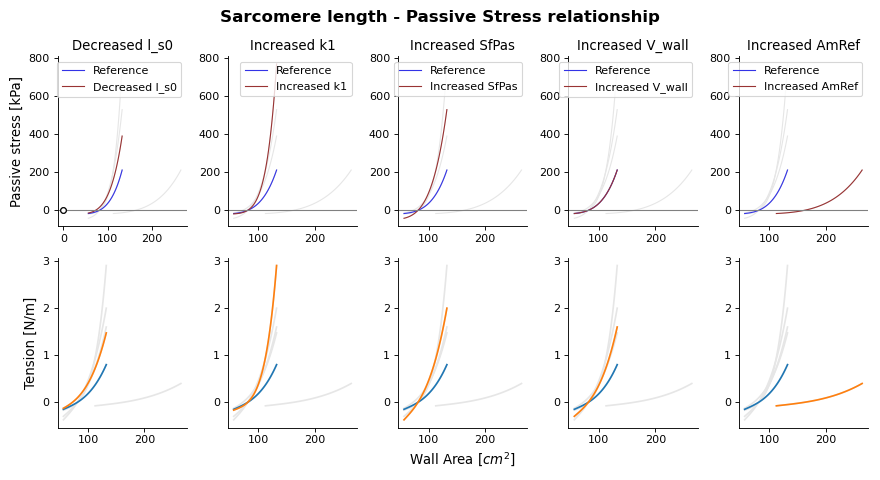
Passive stress-strain relation as function of wall area

Assumptions

Not Included in this Version of the Model:

• Force-frequency relationship (force of contraction increases with heart rate).

• Electrophysiology model, only imposed activation times.

• Biophysics / energetics of calcium transient, cross-bridge formation, etc - currently, this is modelled phenomenologically and availability of ATP is assumed to be infinite.

• Sympathetic / para-sympathetic stimulation of cardiomyocytes.

References

[Walmsley2015]

A citation (as often used in journals).