Tags: ArtVen Tube0D

Verification of ArtVen and Tube0D

In order to verify the ArtVen and Tube0D, a benchmark model is designed in which the ArtVen is placed inbetween two Tube0D cavities with different initial volume conditions.

Code Verification of the State Variables \(V\) of Tube0D in interaction with ArtVen

In this model setup, it holds

(1)\[-\frac{dV_{prox}}{dt} = q_{AV} = \frac{dV_{dist}}{dt}\]

This reduces the number of state variables in the analytical solution from two to one.

(2)\[V_{dist} = V_{tot} - V_{prox}\]

The state variable to solve is:

(3)\[\frac{d V_{dist}}{dt} = \text{sign}(Dp) \cdot q_0 \cdot \left( \frac{|Dp|}{p0} \right)^k\]

In the special case of \(k=1\), this results in the solved equation

(4)\[ \begin{align}\begin{aligned}V_{dist} = \frac{V_{prox,0} + V_{dist,0}}{2} + \left(V_{dist, 0} - \frac{V_{prox,0} + V_{dist,0}}{2}\right) \cdot e^\frac{-t}{\tau}\\\tau = l A_{wall} \frac{p_{0,artven} }{ p_{0,tube0D} } \frac{(A_0/A_{wall}+0.5) }{ q_{0,artven}}\end{aligned}\end{align} \]

Verification

(Source code, png, hires.png, pdf)

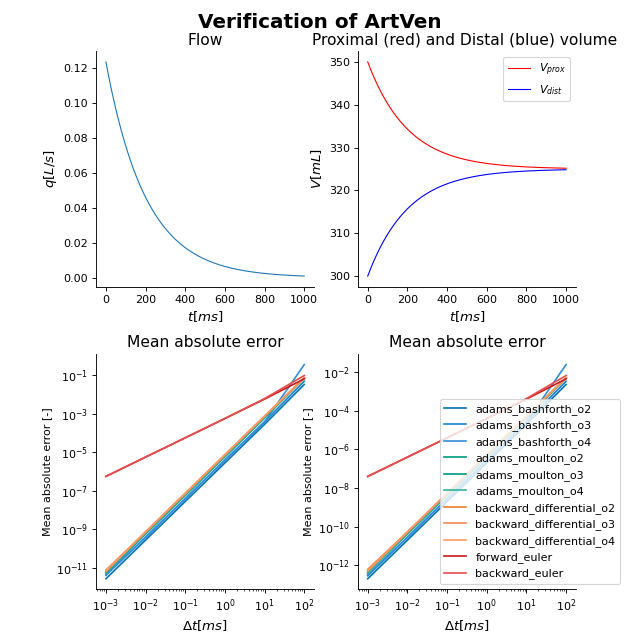
Fig. 20 Verification of the ArtVen module. Left: True solution of the flow pattern (solid) with the forward euler solution at \(\Delta t = 5e-3ms\). Right: Mean L2 error, defined as \(\sum_t \frac{\Delta t}{t_{cycle}} \frac{q_{true}(t) - q_{model}(t)}{\overline{q_{true}}}\), as a function of the timestep \(\Delta t\) for different numerical solvers. At \(\Delta t = 1ms\), all numerical solvers have mean L2 \(<1e-2\).