Chamber

Module summary

Tags: Chamber

Chamber is a thick-walled sphere with a Wall describing the pressure \(p=f(A_m, C_m)\).

Parameters

buckling: bool

Buckling function. If True, wall tension cannot be below zero.

Signals

V [m ³]: array

Volume of the Cavity

p [Pa]: array

Pressure in the Node

Background

The one-fiber model Arts et al.[1] simulates a pressurized cavity encapsulated by a wall composed of fibers, immersed in a soft incompressible material. Within the CircAdapt framework, the one-fiber model is calculated on the mid-wall of the Wall object. The Chamber module translates its state variable \(V\) (cavity volume) into the regional variable \(A_m\) (mid-wall area).

Module description

The Chamber is implemented as a Cavity, meaning that the pressure is given by

(1)\[p = p_{extern} + p_{trans} + \frac{q}{Z},\]

in which the external pressure \(p_{extern}\) comes from the (optional) surrounding cavity and the transmural pressure \(p_{trans}\) is calculated by the \(Wall\) module. The wave impedance \(Z\) is based on Wall properties and defined by

(2)\[p = p_{extern} + p_{trans} + \frac{q}{Z},\]

Wave impedance

Todo

derive wave impedance.

Anti Collapse

To prevent the Chamber to fully empty, an additional anti-dollapse pressure is added.

(3)\[ \begin{align}\begin{aligned}V_{N,lo} = \max(V / V_{wall}, eps)\\\sqrt{\Delta p _{lo}} = \max(0, 0.5 / V_{N,lo} - 1)\\p_{trans}^* = p_{trans} - 1220 \Delta p _{lo}\end{aligned}\end{align} \]

This equation behaves as depicted in the figure below.

(Source code, png, hires.png, pdf)

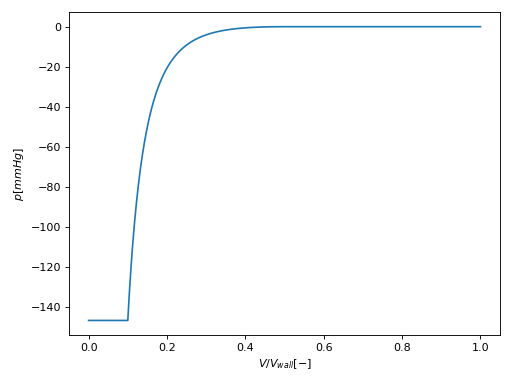
Fig. 3 Additional pressure as function of \(V/V_{wall}\) to prevent collapse.

Old

The one-fiber model [Arts 1991] simulates a pressurized cavity encapsulated by a wall composed of fibers, immersed in a soft incompressible material. Below, the model is presented briefly. The major assumption is that mechanical energy generated by myofibers dE_f is converted into pump function of the cavity dE_v. without any loss of energy. We define wall shell volume \(Vsh\), myofiber stress \(\sigma_f\), natural myofiber strain \(\epsilon_f\), cavity pressure p and midwall enclosed volume \(V_m\). It holds:

(4)\[V_sh \sigma_f d\epsilon_f = dE_f = dE_v = p dV_m (1)\]

Considering Vsh to be small relative to Vm,, a relative change in fiber strain equals one-third of the relative change in volume, resulting in:

(5)\[ d\epsilon_f = \frac{dV_m}{3V_m}\]

Combining the latter two equations, fiber stress is coupled to cavity pressure:

(6)\[ p=\sigma_f \frac{V_{sh}}{3V_m}\]

To accommodate inhomogeneity of mechanical properties in the wall, we modified our approach by inserting Patch-modules, forming together a wall. Linearized mechanical properties of the wall composed of patches are described with a given zero tension mid-wall area \(A_{m,0}\) and wall stiffness \(dT_m/dA_m\). For wall tension T it is found:

(7)\[ T_m = \frac{dT_m}{dA_m}(A_m-A_{m, 0})\]

In this equation, A_{m,0} and frac{dt}{dA_m} are calculated using the Wall2022 component. At low tension, myocardial fibers may buckle. This model has the option ‘buckling’, which replaces this equation with

(8)\[ T_m = \frac{dT_m}{dA_m}(\max(0, A_m-A_{m, 0}))\]

The Chamber and TriSeg-module are designed to render cavity pressure(s) as a function of cavity volume(s), given zero-tension area \(A_{m,0}\) and wall stiffness \(dT_m/dAm\).

A chamber consists of a cavity with cavity volume Vc, wall volume Vw, zero tension midwall area \(A_{m,0}\) and wall stiffness \(dT_m/dA_m\). For the primary derivation we use the assumption that the mid-wall surface is spherical with radius r. Using that the mid-wall surface encloses cavity volume and half wall volume, for mid-wall area Aw it holds:

(9)\[ A_m=(6 \sqrt\pi V_m)^\frac{2}{3} \text{ with } V_m=V_c+\frac{1}{2} V_w\]

Using Eq.(.) wall tension T is determined. Wall tension T and pressure pc are related by the following equation:

(10)\[ T_m \cdot dA_m = p dV_m\]

Using \(A_m=4\pi r^2\) and \(V_m=4\pi r^3 / 3\), Eq. (7) renders cavity pressure \(p_c\):

(11)\[ p_c = \frac{2T}{r} \text{ with } r=(\frac{3V_m}{4\pi})^\frac{1}{3}\]

Since pressure \(p_c\) is written as a function of \(V_c\) and \(V_w\), just like with the one-fiber model, the thus calculated pressure is likely to be not very sensitive to differences in geometry, i.e., geometry may differ from spherical.

References

[1]

Theo Arts, PH Bovendeerd, Frits W Prinzen, and Robert S Reneman. Relation between left ventricular cavity pressure and volume and systolic fiber stress and strain in the wall. Biophysical journal, 59(1):93–102, 1991.

circadapt.components.cavity.Chamber(...[, ...])

Chamber is a thick-walled sphere with a Wall describing the pressure \(p=f(A_m, C_m)\).